Table Of Content
The row effect is the order of treatment, whether A is done first or second or whether B is done first or second. So, if we have 10 subjects we could label all 10 of the subjects as we have above, or we could label the subjects 1 and 2 nested in a square. This is similar to the situation where we have replicated Latin squares - in this case five reps of 2 × 2 Latin squares, just as was shown previously in Case 2.
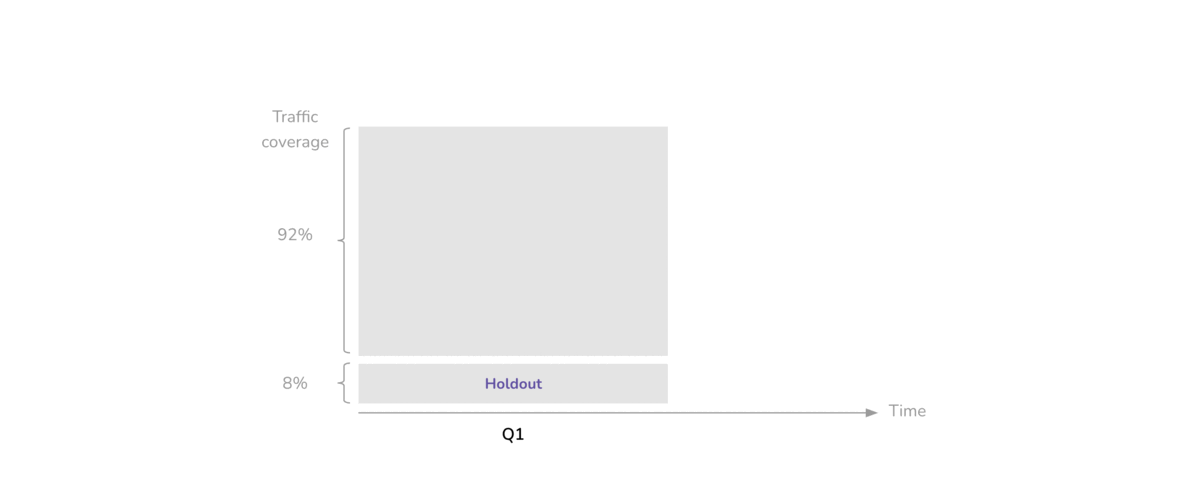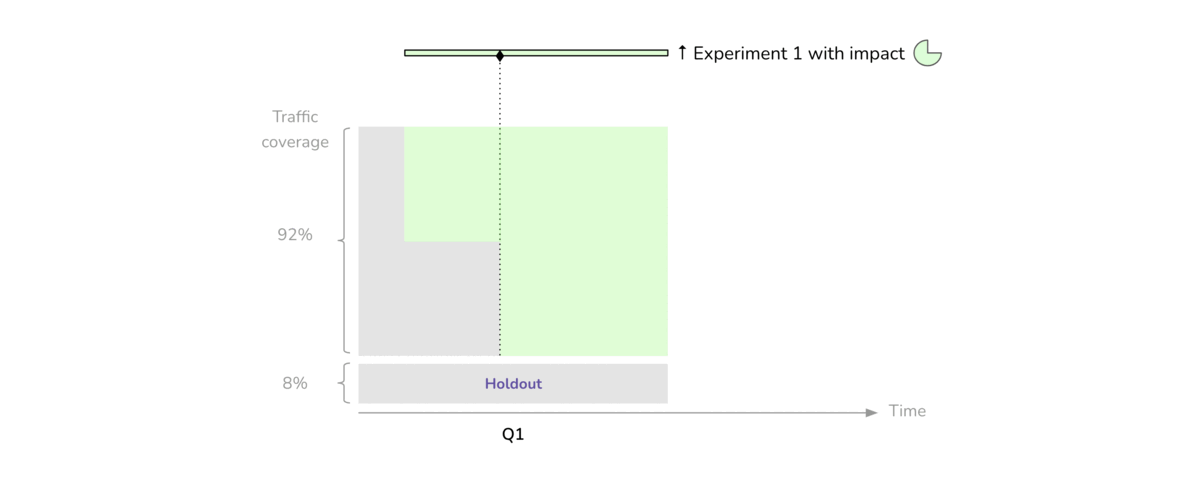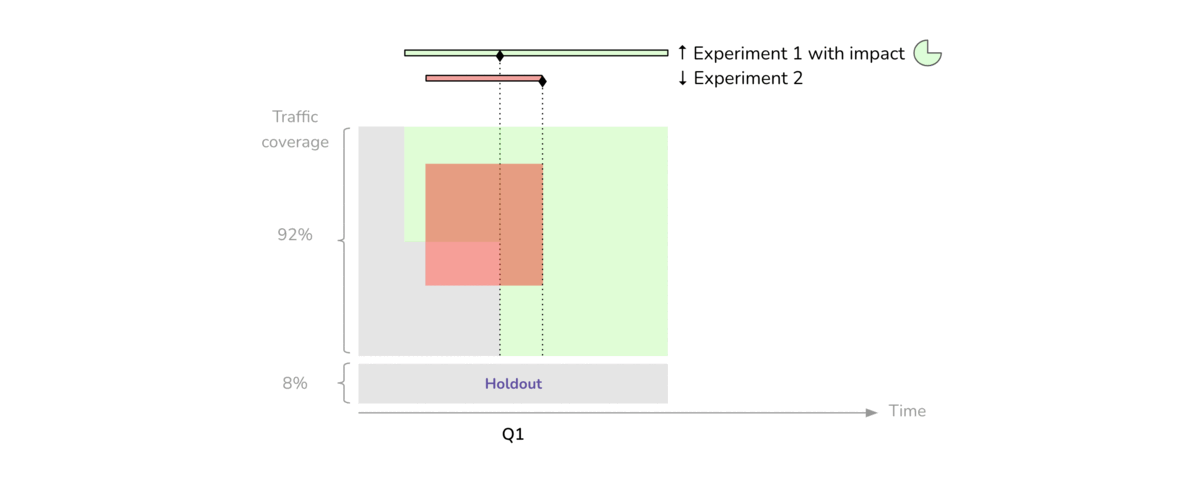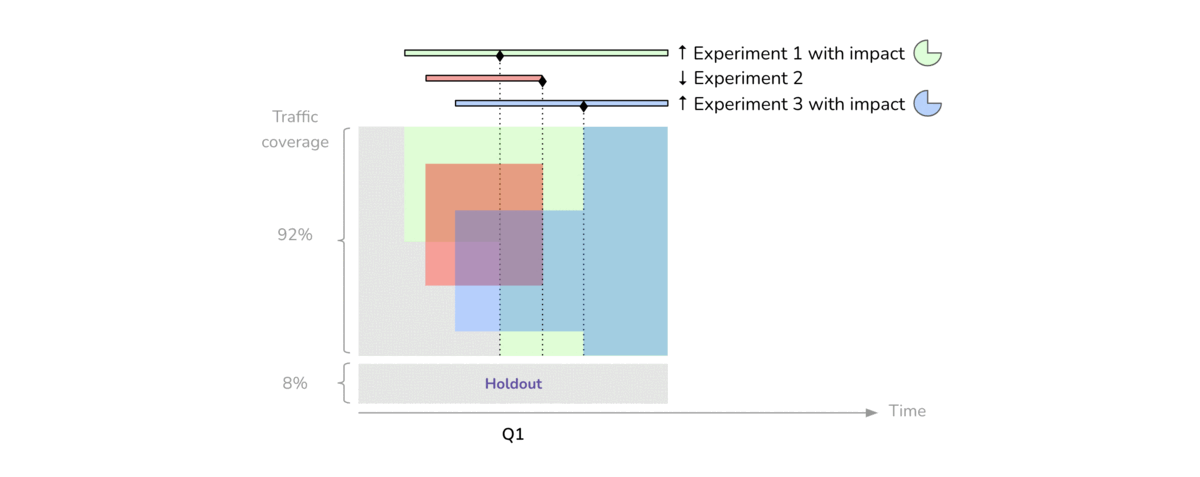
Balanced Incomplete Block Design (BIBD)
It depends on the conditions under which the experiment is going to be conducted. This is a simple extension of the basic model that we had looked at earlier. The row and column and treatment all have the same parameters, the same effects that we had in the single Latin square.
Why have I been blocked?
A Refresher on A/B Testing - HBR.org Daily
A Refresher on A/B Testing.
Posted: Wed, 28 Jun 2017 07:00:00 GMT [source]
To randomize, first randomly permute the order of the rows and produce a new square. We could select the first three columns - let's see if this will work. Click the animation below to see whether using the first three columns would give us combinations of treatments where treatment pairs are not repeated. Is the period effect in the first square the same as the period effect in the second square?
Performance Analysis of Shunt Network for Adaptive Optical Hybrid Interconnection
First we discuss what blocking is and what its main benefits are. After that, we discuss when you should use blocking in your experimental design. Finally, we walk through the steps that you need to take in order to implement blocking in your own experimental design. While you're building your confidence, it never hurts to think about how you might have to block a process you'd like to study. If you do, you can feel more confident knowing you can account for these variables with blocks.
It is just a question about what order you give the treatments. The smallest crossover design which allows you to have each treatment occurring in each period would be a single Latin square. Many times there are nuisance factors that are unknown and uncontrollable (sometimes called a “lurking” variable). We always randomize so that every experimental unit has an equal chance of being assigned to a given treatment. Randomization is our insurance against a systematic bias due to a nuisance factor.
In this case, the test specimens would be considered a source of nuisance variability. If we conduct this as a blocked experiment, we would assign all four tips to the same test specimen, randomly assigned to be tested on a different location on the specimen. Since each treatment occurs once in each block, the number of test specimens is the number of replicates. When we have a single blocking factor available for our experiment we will try to utilize a randomized complete block design (RCBD). We also consider extensions when more than a single blocking factor exists which takes us to Latin Squares and their generalizations.

5 - What do you do if you have more than 2 blocking factors?
We consider this case later, but it does not change the test for a treatment effect. The test on the block factor is typically not of interest except to confirm that you used a good blocking factor. The Analysis of Variance table shows three degrees of freedom for Tip three for Coupon, and the error degrees of freedom is nine. In this experiment, each specimen is called a “block”; thus, we have designed a more homogenous set of experimental units on which to test the tips. To conduct this experiment we assign the tips to an experimental unit; that is, to a test specimen (called a coupon), which is a piece of metal on which the tip is tested. In this article we tell you everything you need to know about blocking in experimental design.
Abstract
So what types of variables might you need to balance across your treatment groups? Blocking is most commonly used when you have at least one nuisance variable. A nuisance variable is an extraneous variable that is known to affect your outcome variable that you cannot otherwise control for in your experiment design.
Nuisance variables
Use the viewlet below to walk through an initial analysis of the data (cow_diets.mwx | cow_diets.csv) for this experiment with cow diets. In this Latin Square we have each treatment occurring in each period. Even though Latin Square guarantees that treatment A occurs once in the first, second and third period, we don't have all sequences represented.
Since \(\lambda\) is not an integer there does not exist a balanced incomplete block design for this experiment. Seeing as how the block size in this case is fixed, we can achieve a balanced complete block design by adding more replicates so that \(\lambda\) equals at least 1. It needs to be a whole number in order for the design to be balanced.
A 3 × 3 Latin square would allow us to have each treatment occur in each time period. We can also think about period as the order in which the drugs are administered. One sense of balance is simply to be sure that each treatment occurs at least one time in each period. If we add subjects in sets of complete Latin squares then we retain the orthogonality that we have with a single square.
Below is the Minitab output which treats both batch and treatment the same and tests the hypothesis of no effect. We can use the Minitab software to construct this design as seen in the video below. You can email the site owner to let them know you were blocked. Please include what you were doing when this page came up and the Cloudflare Ray ID found at the bottom of this page.
To achieve replicates, this design could be replicated several times. Here is a plot of the least squares means for Yield with the missing data, not very different. Generally the unexplained error in the model will be larger, and therefore the test of the treatment effect less powerful. Then, under the null hypothesis of no treatment effect, the ratio of the mean square for treatments to the error mean square is an F statistic that is used to test the hypothesis of equal treatment means.
This form of balance is denoted balanced for carryover (or residual) effects. We want to account for all three of the blocking factor sources of variation, and remove each of these sources of error from the experiment. The Greek letters each occur one time with each of the Latin letters. A Graeco-Latin square is orthogonal between rows, columns, Latin letters and Greek letters.
“k”, “l” and “m” are indices for the different treatment factors. Note that the least squares means for treatments when using PROC Mixed, correspond to the combined intra- and inter-block estimates of the treatment effects. As the treatments were assigned you should have noticed that the treatments have become confounded with the days.
Days of the week are not all the same, Monday is not always the best day of the week! Just like any other factor not included in the design you hope it is not important or you would have included it into the experiment in the first place. Because of the restricted layout, one observation per treatment in each row and column, the model is orthogonal.

No comments:
Post a Comment